Economists Anna Stansbury and Larry Summers released a new paper today, “Productivity and Pay: Is the Link Broken?” which explores the relationship between economic productivity and compensation.

We welcome further inquiry into the relationship between productivity growth, inequality, and the ability of typical workers to benefit from a growing economy—and what policies are needed to do that. The Stansbury/Summers analysis adds some light but also some confusion and, ultimately, makes oversized claims about the role of productivity, especially since minor changes in specification of one of the three variables—unemployment—both substantially weakens some of their results, and also highlights just what is being missed in this investigation.

What are the issues?

The iconic chart (data here) that Stansbury and Summers are investigating is one showing a typical workers’ hourly compensation (measured as the compensation for production/nonsupervisory workers, roughly 80 percent of payroll employment) grew in tandem with productivity in the 1948-73 period but diverged thereafter. We have presented decompositions of the wedges between productivity and compensation for a typical worker that identifies the contribution to the divergence of: 1) changes of labor’s share of income (gap between average productivity and average compensation); 2) changes in wage/compensation inequality (gap between typical worker’s compensation and average compensation); and 3) differences in price deflators used for productivity and compensation. We find in the most recent period, 2000-2014, that rising inequality—both compensation inequality and reductions in labor’s income share—explains eighty percent of the gap between productivity and a typical workers compensation.

The Stansbury/Summers paper does not dispute any of our data, or the key finding that there has been a substantial gap between the growth of productivity (net of depreciation) and the hourly compensation of a typical worker since 1973. Productivity since then has grown 73 percent, while a typical worker’s compensation grew about 12 percent (using either median hourly compensation or the production worker series). Even if one measures this with alternative price indices the same overall picture remains. These data imply that a typical worker received only a small share of all the productivity growth generated over the past four decades.

Stansbury/Summers set out to examine whether productivity is linked to compensation growth, on average and for a typical worker, using the data we provided. We would stress that our findings on this topic have always focused on the gap between a typical workers’ pay and productivity, which is why the title of our recent paper was “Understanding the Historic Divergence Between Productivity and a Typical Worker’s Pay: Why It Matters and Why It’s Real.” Unfortunately, far too much of the Stansbury/Summers paper and its press coverage so far glosses over the crucial distinction in a world of continuous rising wage inequality between average and typical workers’ compensation.

Stansbury and Summers examine whether increases in productivity translate seamlessly into higher compensation on average or for typical workers. Conventional economic analysis and punditry often asserts by assumption that there is a 1-to-1 link between these two. So, any wage problem that arises inspires only one policy diagnosis: make productivity grow more rapidly. Our argument has simply been that productivity is a necessary, but not sufficient, condition for broad-based wage growth. But if other policy decisions are made with the aim of suppressing wage growth for typical workers, pay can stagnate even as productivity rises. In the end, nothing in the Stansbury/Summers analysis makes us rethink this view. Instead, their results simply show that there may be a link (though generally not one-for-one) between productivity and a typical worker’s pay, holding everything else equal. This finding does not support a claim that policymakers should only focus on productivity growth if they want wages to rise.

What did Stansbury and Summers find?

Given the previous discussion, we will focus now only on the Stansbury/Summers findings regarding the links between productivity and pay for production and non-supervisory workers. Again, our claim isn’t that overall average pay has lagged terribly far behind productivity, it’s that pay for most workers has, and that the average has been kept up by a large redistribution of pay to the high end (think CEOs and financial sector professionals). Production and non-supervisory workers constitute 80 percent of the private-sector workforce.

In Table 1 of their paper, Stansbury and Summers present results from regressing the 3-year average of hourly production worker pay on the 3-year average of productivity growth, controlling for changes in unemployment. They find that over the entire 1950-2014 period, the coefficient on productivity growth is 1, implying all else equal (this is very important) each 1 percent increase in productivity raises pay by 1 percent. When splitting this into two sub-samples, 1950-1973 and 1975-2014, they find a slightly smaller, but still large and statistically significant coefficient on productivity. Most surprisingly, it is an identical 0.6 in each sub-period.

At first blush, this seems like a big challenge to our claim that the link between productivity and pay has been radically weakened since the late 1970s. But it’s really not. A regression coefficient shows the all-else-equal effect of one variable on another. So, it could well be true that after the mid-1970s, productivity growth was indeed “trying” to boost wages and that if only productivity had changed over that time that wages would have risen smartly.

But our claim is simply that “all else” was not equal after the mid-1970s. To illustrate what this means, consider one technical tweak to the Stansbury/Summers regression: adding the unemployment rate as a level, rather than change, into their regression of production worker pay on productivity. The table below shows coefficients from an almost-identical regression to the Stansbury/Summers results in Table 1, columns 1e-1g (the difference is how we deflate production worker pay, but that doesn’t end up changing the regression in any significant way). With just productivity growth and the change in unemployment, the Stansbury/Summers results are essentially replicated.

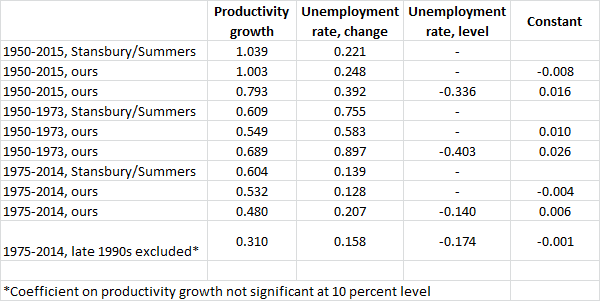
But it’s far more standard to regress compensation growth on unemployment levels and productivity (say in standard wage Phillips curves) than to use the unemployment change. Adding unemployment as a level actually pushes up the coefficient on productivity in the earlier period and pushes down the coefficient in the latter period, but that’s less important.

More important is that the coefficient on unemployment is large and negative—higher unemployment rates are associated with slower pay growth. This is not surprising. But then consider the average unemployment rate in 1950-1973 compared to 1975-2014; it’s about 1.8 percentage points higher in the second period. So, if one compares the effect of productivity plus unemployment rather than just the effect of productivity, it’s clear that one would predict that pay growth would be slower in the second period (and reminder: it was).

Further, the constant term that results after adding in unemployment as a level is interesting. In the earlier period, this constant term indicates that trend pay growth (pay growth that would’ve resulted had the variables included in the regression not moved at all) in the earlier period was 2.5 percent, while it was essentially zero in the later period.

So, again, maybe productivity growth was indeed all-else-equal trying to push up hourly pay in the latter period, and with the same force it applied in earlier periods. But we know it failed. Pay growth decelerated markedly after the mid-1970—far more than did productivity growth (and these facts are not disputed).

It also seems that Stansbury and Summers have moved the goalposts. They tout that they find a link between productivity and the pay of a typical worker, even though that link is often in their regressions not the oft-claimed 1-to-1 linkage. The linkage is 0.6-to-1 in their work and falls to 0.5-to-1 when one adds unemployment levels. But these linkages are not even present when we omit the late 1990’s period of accelerating productivity and wage growth: the linkage falls to a statistically insignificant 0.3-to-1. This suggests that modesty is in order about claims that there is any tight and proportional link between productivity and the compensation of a typical worker.

Our contention all along has been that this pay deceleration did not just reflect slower productivity growth, but that it in fact reflected a number of intentional policy decisions that undercut typical workers’ ability to demand and achieve higher pay. One such policy decision was exactly over how aggressively the Federal Reserve and other macroeconomic policymakers should target low unemployment. Others included decisions about whether or not to protect workers’ rights to organize and bargain collectively (the country obviously chose not to) and whether or not to raise the federal minimum wage in line with inflation or productivity growth (again, we chose not to).

In the end, our argument was never about what a regression coefficient would show about the all-else-equal association between productivity and pay. It has instead been about everything that was not kept equal in regards to pay-setting since the mid-1970s. As non-productivity influences on pay were systematically rigged to suppress wages, pay failed to rise even as productivity did. This should be a key concern for policymakers, regardless of the value of a regression coefficient.

What does all this mean to policy?

In regards to the claim that Stansbury and Summers are disputing, let’s go back to our 2015 paper that they quote: “…boosting productivity growth…will not lead to broad-based wage gains unless we pursue policies that reconnect productivity growth and the pay of the vast majority.” This still seems right-on to us. It’s not an argument to not try to raise productivity growth. It’s an argument that many things besides productivity influence typical workers’ pay, and if they’re manipulated to rob these workers of leverage, pay growth can absolutely stagnate even if productivity rises.

What one of us wrote the Wall Street Journal’s Greg Ip when asked for our take for his story today is a decent summing-up:

To be really concrete, if (say) the next 15 years sees decent productivity growth (say 1.5 percent annually or above) but is characterized by the 6.5 percent average unemployment rate that characterized the 1979-2015 period, and we see no fundamental change in workers’ organization, I think we’ll see truly miserable wage growth for the majority of workers (basically the 0.2 percent growth that characterized the 1979-2013 period for the bottom 70 percent). If instead we see average unemployment lower than 5 percent, and see some growth in workers covered by a collective bargaining agreement and some ambitious increases in minimum wages, I think we can make typical workers’ pay and productivity move a lot closer together.

In the end, it seems that Stansbury and Summers are saying the same thing as we do. Ip summarizes their point as “[Stansbury/Summers] found a strong and persistent link between hourly productivity and a variety of wage measures since 1973. The problem, they conclude, is that the positive influence of productivity on pay has been overwhelmed by other forces pushing the other way.” That, in fact, sounds the same as our conclusions, and from the point of view of a typical worker is the same: if we raise productivity but do not address policies that escalate inequality—Stansbury and Summers’ “other forces”—then those productivity augmenting policies will fail to result in higher living standards for typical workers.